Πολλαπλασιασμός ακεραίων αριθμών με έξυπνη χρήση άλγεβρας και Τεχνικές πολλαπλασιασμού ακεραίων αριθμών ή και τετράγωνο ακεραίου αριθμού με ταχύτητα.

Πόσοι από μας κάνουν πράξεις πολλαπλασιασμού ακεραίων αριθμών λάθος;
Οι περισσότεροι κάνουν πολλαπλασιασμό ακεραίων αριθμών όπως τους έδειξαν οι γονείς τους αγνοώντας όσα έμαθαν στο δημοτικό ή στο γυμνάσιο.
Αντίθετα με όσα πιστεύουμε όμως για τον εαυτό μας, τελικά αυτοί οι τρόποι δεν είναι πάντα οι ενδεδειγμένοι.
Τι θέλουμε να τονίσουμε με αυτό όχι μόνο για τον πολλαπλασιασμό;
Φυσικά, ότι πάντα ο εχθρός του καλού είναι το καλύτερο. Εφόσον μπορούμε να εκμεταλλευτούμε κάποιες αλγεβρικές ιδιότητες, γιατί να μην το τολμήσουμε; Θα γλυτώσουμε πολύ χρόνο.
Γιατί άραγε να σπαταλάμε φαιά ουσία και κυρίως να χάνουμε την ελευθερία μας;
Και όμως χάνεται!
Πώς χάνεται η ελευθερία μας στον πολλαπλασιασμό ακεραίων αριθμών;
Είναι προφανές ότι χρησιμοποιώντας για πολλαπλασιασμούς ή διαιρέσεις μόνο το κομπιουτεράκι χάνουμε την ελευθερία μας.
Σύμφωνα με τα προηγούμενα η εξάρτηση από τη μηχανή γίνεται ολοένα και μεγαλύτερη.
 Για τον υπολογισμό του τόκου του τόκου στη λήξη 12μηνης τραπεζικής επένδυσης σταθερού επιτοκίου ενός αρχικού κεφαλαίου τί κάνουμε;
Για τον υπολογισμό του τόκου του τόκου στη λήξη 12μηνης τραπεζικής επένδυσης σταθερού επιτοκίου ενός αρχικού κεφαλαίου τί κάνουμε;
Τί κάνουν οι περισσότεροι; Απλούστατα, ανατρέχουν σε ένα excel και βάζουν τη συνάρτηση... Γιατί το κάνουν αυτό; Μα φυσικά, διότι ούτε και τον τύπο εξαγωγής του τόκου για ένα κεφάλαιο με συγκεκριμένο επιτόκιο, σταθερό για ένα χρόνο, δεν μπορούν να θυμηθούν.
Ισχυρισμός: Οι περισσότεροι πολλαπλασιασμοί διψήφιων ακεραίων αριθμών καταλήγουν σε διαφορά τετραγώνων ακεραίων ή γίνεται χρήση τετραγώνου αριθμού που λήγει σε πέντε (5).
Παράδειγμα1: Υπολογισμός τόκου στη λήξη 12μηνης τραπεζικής τοποθέτησης με σταθερό επιτόκιο 2,1% για αρχικό κεφάλαιο 19.000 Ευρώ.
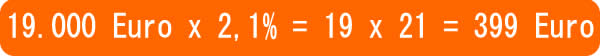
Στην πραγματικότητα, εκείνο που απομένει είναι ένα γινόμενο 2 ακεραίων αριθμών, που στην πλειονότητα των περιπτώσεων είναι ένα γινόμενο 2 διψήφιων ακεραίων αριθμών.
Τί χρειάζεται να γίνει; Να μάθουμε να σκεφτόμαστε αλλιώς!!! Το γινόμενο 2 διψήφιων ακεραίων υπόκειται σε ορισμένες αλγεβρικές ιδιότητες. Όλοι θυμόμαστε τη διαφορά τετραγώνων.
Για άλλο τρόπο σκέψης, ταχύτερο και αποτελεσματικότερο για την καθημερινότητά σας δείτε το επόμενο βίντεο, που εξηγεί την εφαρμογή της αλγεβρικής ιδιότητας της διαφοράς τετραγώνων.
Παράδειγμα2: Υπολογισμός τόκου στη λήξη 12μηνης τραπεζικής τοποθέτησης με σταθερό επιτόκιο 4,5% για αρχικό κεφάλαιο 45.000 Ευρώ.

Για το τέχνασμα της εύρεσης 45x45=2025 αλλά και οποιουδήποτε τετραγώνου ακεραίου αριθμού που λήγει σε πέντε (252,352,...,952,1052,1152,...,10052,10152,10252,...) εν ριπή οφθαλμού δείτε το επόμενο βίντεο:
Αφού είδατε τα προηγούμενα βίντεο πιστεύετε ότι μπορείτε να πειραματιστείτε στην ταχύτητα πράξεων; Δείτε το επόμενο Link για τεχνικές πολλαπλασιασμού ακεραίων και θα εκπλαγείτε για την ευκολία που υπάρχει στην εκτέλεση του πολλαπλασιασμού, που μέχρι τώρα αγνοούσατε.









